- Taylors Lehrsatz
Taylors Lehrsatz, benennt nach Taylor 4), eine der wichtigsten Grundlagen der Differentialrechnung u. ihrer Anwendungen, ist ein Satz, welcher den Werth einer Function y – f (x), welchen dieselbe annimmt, wenn die unabhängig veränderliche Größe x um einen positiven od. negativen Betrag h zunimmt, also den Werth f (x + h) in eine Reihe zu entwickeln lehrt, welche nach Potenzen von h fortschreitet u. außerdem nur noch den Werth der Function u. ihrer Differentialquotienten für den Anfangswerth x nebst constanten Coefficienten enthält. Sie wird gewöhnlich in folgender Form gegeben
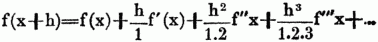
wo nach Lagrange's Bezeichnung f' (x) = dy/dx, f''(x) = d2y/dx2 etc. Die Gültigkeit dieser Taylorschen Reihe ist jedoch an gewisse Bedingungen geknüpft, Nennt man nämlich y, = y + Δx den Werth, welchen die Function y annimmt, während die unabhängig Veränderliche = x + Δx wird, ferner y2 – y1 + Δy, den zu x + 2 Δx, y3 = y2 Δy2 den zu x + 3 Δx gehörenden Werth der Function etc., bezeichnet man ferner die Differenz Δy1 – Δy durch Δ2y ebenso Δ2y1 durch Δ3x etc., so ergibt sich sofort y2 = y + 2 Δy + Δ2y, y3 = y + 3 Δy + 3 Δ2y + Δ3y u. allgemein
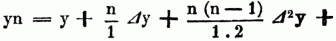
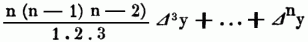
hierin ist y n = f (x + n Δx). Nun kann man statt n Δx den einfachen Buchstaben h einsetzen, folglich rechter Hand
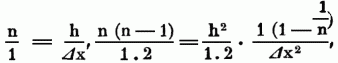
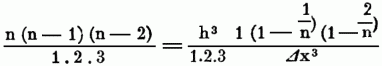
setzen; u. da die Größen von Δx u. n willkürlich genommen werden können, so kann man, während n Δx eine endliche Größe h bleibt, Δx als unendlich klein u. n als unendlich groß annehmen, vorausgesetzt, daß keins der Glieder rechter Hand durch diese Annahme unendlich wird. Da nun
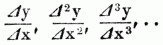
bei verschwindend kleinem Δx in die Differentialquotienten dy/dx, d2y/dx2 ... übergehen, so hat man f (x + h) = f (x)
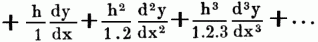
in inf. vorausgesetzt, daß kein Differentialquotient unendlich groß wird. Wenn daher der Werth einer Function u. ihrer Differentialquotienten für einen einzigen Werth des unabhängig Veränderlichen gegeben sind, so kennt man durch diese Reihe[310] auch den Werth der Function für jeden andern Werth der letztren. Da jedoch streng genommen die Reihe dis ins Unendliche fortzusetzen ist, bei den praktischen Anwendungen auf Geometrie u. Mechanik dagegen bei irgend einem Gliede abgebrochen werden muß, so ist es noch nothwendig, die Grenze des Fehlers (d.h. die mögliche Größe des Fehlers) zu bestimmen, welchen man begeht, indem man die folgenden Glieder wegwirft. Dieselbe geht am einfachsten aus folgender Betrachtung hervor: Gesetzt man wollte sich bei der Berechnung von f (x + h) auf die beiden ersten Glieder allein beschränken, so daß man setzte f (x + h) = f (x) + h/1 f′ (x) u. man sagt, der dabei begangene Fehler beträgt noch nicht [h2/(1.2)]P wo P vorläufig noch unbekannt ist, so ist f (x + h) – f (x) – (h/1) f' (x) – [h2/(1.2)]P < 0. Nun gilt ganz allgemein: Wenn irgend ein von h abhängiger Ausdruck für h = 0 selbst = 0 wird, der Differentialquotient dieses Ausdrucks in Bezug auf h aber für dieses Intervall zwischen 0 u. h immer negativ bleibt, so ist dieser Ausdruck selbst nothwendig kleiner als Null. Da nun die linke Seite der zuletzt genannten Ungleichung für h = 0 in der That Null wird, so geschieht ihr Genüge, wenn
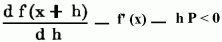
u. dieser Ungleichung wieder geschieht Genüge, wenn
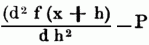
zwischen h = 0 u. h = h immer negativ bleibt, d.h. wenn P den größten Werth bedeutet, welchen der zweite Differentialquotient von f (x + h) nach h zwischen x u. x + h annehmen kann. Nun ist es gleichgültig, ob man f (x + h) nach h od. nach x differentiirt, u. der größte Werth des Differentialquotienten im ganzen Intervall kann bezeichnet werden durch
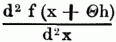
wo Θ ein positiver echter Bruch ist; mithin ist die Grenze des begangenen Fehlers, wenn man beim zweiten Gliede abbricht
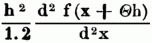
ganz ebenso ist die Fehlergrenze, wenn man beim ersten Gliede abbricht (hn)/(1.2..n)
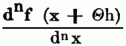
u. dieser Ausdruck heißt der Rest der Taylorschen Reihe. Taylor machte diesen Satz in seiner Methodus incrementorum directa et inversa, Lond. 1715, zuerst bekannt.
Pierer's Lexicon. 1857–1865.
