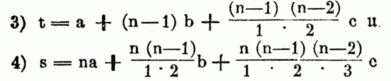Arithmetische Reihe — Arithmetische Reihen sind spezielle mathematische Reihen. Eine arithmetische Reihe ist die Folge, deren Glieder die Summe der ersten n Glieder (den Partialsummen) einer arithmetischen Folge sind. Arithmetische Reihen sind im allgemeinen divergent … Deutsch Wikipedia
Arithmetische Reihe — Arithmētische Reihe oder arithmetische Progression, s. Reihe. Arithmetisches Mittel, s. Mittel. Arithmetische Zeichen, s. Mathematische Zeichen … Kleines Konversations-Lexikon
Arithmetische Reihe — oder Progression der ersten Ordnung ist eine Folge gleichartiger Größen (Glieder der Reihe), deren jede von der vorhergehenden um eine gegebene Größe unterschieden ist; sie heißt steigend oder fallend, je nachdem ihr Unterschied additiv oder… … Herders Conversations-Lexikon
Arithmetische Reihe — Arithmetische Reihe, s. Reihen … Meyers Großes Konversations-Lexikon
Arithmetische Reihen — sind spezielle mathematische Reihen. Eine arithmetische Reihe ist die Folge, deren Glieder die Summe der ersten n Glieder (den Partialsummen) einer arithmetischen Folge sind. Arithmetische Reihen sind im allgemeinen divergent. Es interessieren… … Deutsch Wikipedia
Arithmetische Folge — Eine arithmetische Folge oder arithmetische Progression ist eine regelmäßige mathematische Zahlenfolge mit der Eigenschaft, dass die Differenz zweier benachbarter Folgenglieder konstant ist. Also gilt: (rekursive Formel). Das i te Glied ai einer… … Deutsch Wikipedia
Arithmetische Progression — Eine arithmetische Folge oder arithmetische Progression ist eine regelmäßige mathematische Zahlenfolge mit der Eigenschaft, dass die Differenz zweier benachbarter Folgenglieder konstant ist. Also ai + 1 = ai + d (rekursive Formel) Das i te Glied… … Deutsch Wikipedia
Reihe — Rei|he , die; , n; in, außer der Reihe; der Reihe nach; an der Reihe sein; an die Reihe kommen; in Reih und Glied {{link}}K 13{{/link}}; arithmetische Reihe, geometrische Reihe (Mathematik) … Die deutsche Rechtschreibung
Reihe — Reihe, 1) mehre in einer Linie neben einander befindliche Dinge; 2) das Aufeinanderfolgen nach festgesetzter Ordnung; 3) jede Folge von Größen (die Glieder [Termini] derselben genannt), welche nach einem bestimmten Gesetz gebildet sind. Die R n… … Pierer's Universal-Lexikon
Reihe — Reihe, in der Mathematik eine Aufeinanderfolge von nach einem bestimmten Gesetze gebildeten Zahlen, welche die Glieder der R. heißen. Man unterscheidet zunächst arithmetische und geometrische R.n, auch Progressionen (s. d.) genannt. Jene… … Herders Conversations-Lexikon